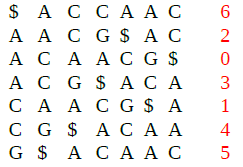4 Burrows-Wheeler: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Auf dieser Seite sind die Themen zusammengeführt, die in Vorlesung 4 am 02.05.2019 behandelt wurden. | Auf dieser Seite sind die Themen zusammengeführt, die in Vorlesung 4 am 02.05.2019 behandelt wurden. | ||
<br> | |||
== Burrows-Wheeler Transformation == | |||
Die Burrows-Wheeler Induzierung wurde in der Informatik ursprünglich zur Optimierung von Daten-Kompression entwickelt.<br> | |||
Sie eignet sich auch gut zur effizienten Suche großer Texte und somit zur Suche eines optimalen Alignments.<br> | |||
<br> | |||
'''Vorteile'''<br> | |||
* Sehr schnell und verbraucht wenig Speicher<br> | |||
* Eine Rücktransformation ist Möglich <br> | |||
* Kein Informationsverlust beim Sortieren<br> | |||
=== Transformation === | |||
Beispiel an der Sequenz T = ACAACG$<br> | |||
'''1. Generierung aller cyclischen Verschiebungen von T'''<br> | |||
Die Sequenz wird cyklisch um eine Stelle verschoben, bis die ursprüngliche Sequenz wieder erreicht ist.<br> | |||
[[File:BWT|thumb|center|Cyklische Rotation]] | |||
In rot ist die 'Suffix-Array' dargestellt. | |||
'''2. Sortierung'''<br> | |||
Die Verschiebung von 'T' wird alphabetisch sortiert, dabei hat das Sonderzeichen (in diesem Fall $) den niedrigsten Wert.<br> | |||
[[File:Bwt sortierung.png|thumb|center|Alphabetische Sortierung]] | |||
Die letzte Spalte wird als '''Burrows-Wheeler Transformation''' (BWT) bezeichnet.<br> | |||
ACAACG$ → CC$AAAC<br><br> | |||
'''Eigenschaften der BWT :'''<br> | |||
<br> | * Hat die gleiche Länge, wie die Originalsequenz <br> | ||
* Originalsequenz T kann direkt aus BWT regeneriert werden | |||
''''Last-First Zuordnung''''<br> | |||
* | Die 'i'te Position des Buchstaben x in der letzten Spalte (Transformation) entspricht der 'i'ten Position in der 1. Spalte<br> | ||
<br> | Benötigt werden nur die erste und letzte Spalte nach der cyklischen Verschiebung.<br> | ||
<br> | |||
<br> | |||
<br> | |||
Revision as of 23:29, 15 May 2019
Auf dieser Seite sind die Themen zusammengeführt, die in Vorlesung 4 am 02.05.2019 behandelt wurden.
Burrows-Wheeler Transformation
Die Burrows-Wheeler Induzierung wurde in der Informatik ursprünglich zur Optimierung von Daten-Kompression entwickelt.
Sie eignet sich auch gut zur effizienten Suche großer Texte und somit zur Suche eines optimalen Alignments.
Vorteile
- Sehr schnell und verbraucht wenig Speicher
- Eine Rücktransformation ist Möglich
- Kein Informationsverlust beim Sortieren
Transformation
Beispiel an der Sequenz T = ACAACG$
1. Generierung aller cyclischen Verschiebungen von T
Die Sequenz wird cyklisch um eine Stelle verschoben, bis die ursprüngliche Sequenz wieder erreicht ist.
In rot ist die 'Suffix-Array' dargestellt.
2. Sortierung
Die Verschiebung von 'T' wird alphabetisch sortiert, dabei hat das Sonderzeichen (in diesem Fall $) den niedrigsten Wert.
Die letzte Spalte wird als Burrows-Wheeler Transformation (BWT) bezeichnet.
ACAACG$ → CC$AAAC
Eigenschaften der BWT :
- Hat die gleiche Länge, wie die Originalsequenz
- Originalsequenz T kann direkt aus BWT regeneriert werden
'Last-First Zuordnung'
Die 'i'te Position des Buchstaben x in der letzten Spalte (Transformation) entspricht der 'i'ten Position in der 1. Spalte
Benötigt werden nur die erste und letzte Spalte nach der cyklischen Verschiebung.